KALKULUS

MATERI KULIAH KALKULUS

Disusun oleh:

Selvia Nuer Agustin, S.Ars.

FAKULTAS SAINS DAN TEKNOLOGI PRODI TEKNOLOGI INFORMASI

UNIVERSITAS IBRAHIMY SUKOREJO SITUBONDO

2019

Rumus Integral Matematika- Dalam matematika ada namanya turunan ada juga namanya integral. Lalu, apa itu integral? Ia adalah lawan dari turunan atau diferensiasi. Sobat di Kelas XII pasti akan mendapatkan materi matematika ini. Integral juga dikenal sebagai antidiferensial dan dilambangkan dengan bentuk :

∫ (integral)

Sebuah fungsi F(X) disebut sebagai integral dari f(x) selagi apabila turunan pertama F'(x) = f(x). Jadi sebuah persamaan jika diturunkan kemudian diintegralkan akan mengahasilkan persamaan seperti bentuk awal.

Contoh Sobat punya persamaan f(x) = x2 + 2x, ketika persamaan itu di turunakan maka akan menghasilkan f'(x) = 2x + 2. Dengan menggunakan integral akan dapat mengembalikan bentuk 2x + 2 ke bentuk x2 + 2x. Jika turunan menurunkan 1 tingkat eksponen dari x2 ke x maka integral akan mengembalikan tingkat eksponen satu tingkat lebih tinggi, misal x menjadi x2, x2menjadi x3, dan seterusnya. Ada dua macam integral yaitu integral tak tentu dan integral tentu.

Integral Tak Tentu

Yang dinamakan integral tak tentu adalah integral yang tidak memiliki batas atas dan bawah. Biasanya hanya berupa integral dari sebuah aljabar matematika. Bentuk integral ini tidak memiliki daerah asal dan tidak memiliki daerah hasil

∫ f(x) dx = F(x) + c

Integral Tentu

Pondasi dasar tentang integral tentu pertama kali diperkenalkan oleh Newton dan Leibinz yang kemudian dieperkenalkan secara modern oleh Riemann. Integral ini memiliki batas atas dan batas bawah. Dalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas tertentu atau menghitung volume benda jika diputar.

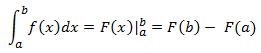
Mengenal Sifat dan Rumus Integral

berikut ini sifat-sifat dari operasi integral

Rumus Dasar Integral

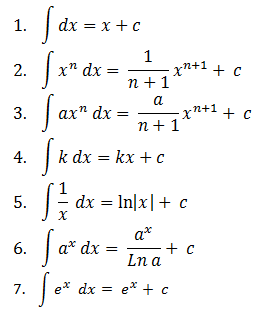
selain rumus dasar di atas, sobat bisa menggunakan rumus cepat lagi praktis

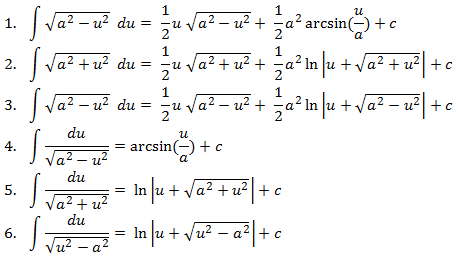
Integral Fungsi Aljabar

Jika ada fungsi aljabar yang diintegralkan maka sobat bisa menggunakan rumus berikut:

contoh, jika sobat punya aljabar 2x + 5 ketika diitegralkan akan mendapatkan hasil sebagai berikut:

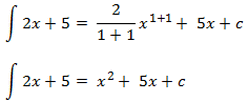
Integral Fungsi Eksponen

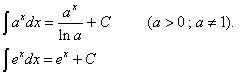
contoh:

∫ 3e4x dx Kita misalkan 4x = u sehingga persamaan di atas menjadi

∫ 3e4x dx = ∫ 3eu du/4

= 3/4 ∫ 3eu du

= 3/4 eu + c

= 3/4 e4x + C

Intgeral Fungsi Trigonometri

berikut rumus integral dari trigonometri yang sering dipakai dalam soal-soal matematika.

a. Integral  dengan variabel sudut x atau sudut ax

∫ sin x dx = – cos x + c

∫ cos x dx =  sin x + c

∫ sin ax dx = – (1/a) cos ax + c

∫ cos ax dx = (1/a) sin ax + c

∫ secs2 x dx = tan x + c

b. Integral dengan Bentuk Pangkat